立体几何

发表于 更新于 分类于 Waline： 阅读次数：

这里记录一些高中数学立体几何实用的解题技巧。

三正弦定理

设二面角$M-AB-N$的角度为$\alpha$，在平面$M$上有一条射线$AC$，它和棱$AB$所成角为$\beta$，和平面$N$所成角为$\gamma$，则$\sin\gamma=\sin\alpha·\sin\beta$.

如图所示

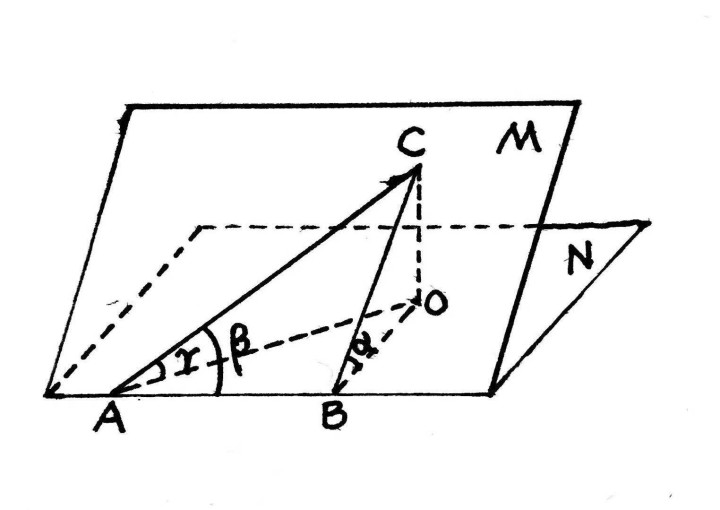
三余弦定理

设$A$为面上一点，过$A$的斜线$AO$在面上的射影为$AB$，$AC$为面上的一条直线，那么$\angle OAC,\angle BAC,\angle OAB$三角的余弦关系为：$\cos \angle OAC=\cos\angle BAC\cdot \cos\angle OAB$($\angle BAC$和$\angle OAB$只能是锐角)，即$\cos\theta=\cos\theta_1\cos\theta_2$.

拓展：将三角形$OAB$以$AB$为轴旋转一定角度，设$O-AB-C=\gamma$，则$\cos\theta=\cos\theta_1\cos\theta_2+\sin\theta_1\sin\theta_2\cos\gamma$.

拟柱体

定义：所有的顶点都在两个平行平面内的多面体叫做拟柱体，它在这两个平面内的面叫做拟柱体的底面，其余各面叫做拟柱体的侧面，两底面之间的垂直距离叫做拟柱体的高。

拟柱体体积公式：设拟柱体的高为$H$，如果用平行于底面的平面$\gamma$去截该图形，所得到的截面面积是平面$\gamma$与一个底面之间距离$h$的不超过$3$次的函数，那么该拟柱体的体积$\boldsymbol{V=\frac16(S_1+4S_0+S_2)\cdot H}$，式中，$S_1$和$S_2$是两底面的面积，$S_0$是中截面的面积(即平面$\gamma$与底面之间距离$h=\frac{H}2$时得到的截面的面积)

其他

  • 任意的简单$n$面体内切球半径为$\boldsymbol{\frac{3V}S}$（$V$ 是简单$n$面体的体积， $S$是简单$n$面体的表面积).
  • 斜二测画法直观图面积为原图形面积的 $\boldsymbol{\frac{\sqrt{2}}{4}}$ 倍.