解析几何
这里记录一些高中数学解析几何实用的解题技巧。
阿基米德三角形
阿基米德三角形:抛物线的弦与过弦的端点的两条切线所围成的三角形。
在抛物线 $y^2=2px$中,弦$|AB|$为阿基米德三角形的底边,$M$为底边的中点,$Q$为两切线的交点。

性质
性质1:阿基米德三角形底边上的中线平行于抛物线的轴.
证明:设$A(x_1,y_1),B(x_2,y_2)$,则$M(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$. 过A点的切线方程$y_1y=p(x_1+x)$,过B点的切线方程$y_2y=p(x_2+x)$. 联立方程$y_1^2=2px_1,y_2^2=2px_2$,解得两交点坐标为$Q(\frac{y_1y_2}{2p},\frac{y_1+y_2}{2})$.
性质2:$\boldsymbol{|AF|\cdot |BF|=|QF|^2}$.
性质3:若阿基米德三角形的底边过焦点$F$,顶点$Q$的轨迹为准线,且阿基米德三角形的面积最小值为$p^2$.
例题
例题1:已知$F$为抛物线$C: x^2=4y$的焦点,过点$F$的直线$l$与抛物线$C$相交于不同的两点$A,B$,抛物线$C$在$A,B$两点处的切线分别是$l_1,l_2$,且$l_1,l_2$相交于$P$,则$|PF|+\frac{32}{|AB|}$的最小值为( ).
解:设 $A(x_1,y_1),B(x_2,y_2)$,直线 $l:y=kx+1$,
联立$\begin{cases} y=kx+1 \\ x^2=4y \end{cases}$ 整理得 $x^2-4kx-4=0$,故 $x_1+x_2=4k,x_1x_2=-4$,
所以 $y_1+y_2=4k^2+2,y_1y_2=1$,
故 $|AB|=y_1+y_2+2=4k^2+4$.
法一:由阿基米德三角形性质2得 $|FA|\cdot |FB|=|PF|^2$.
$\begin{aligned}|PF|&=\sqrt{|FA|\cdot |FB|} \\ &=\sqrt{(y_1+1)(y_2+1)} \\ &=\sqrt{y_1y_2+(y_1+y_2)+1} \\ &=2\sqrt{k^2+1}\end {aligned}$
$\begin{aligned}|PF|+\frac{32}{|AB|}&=2\sqrt{k^2+1}+\frac{8}{k^2+1} \\ &=\sqrt{k^2+1}+\sqrt{k^2+1}+\frac{8}{k^2+1} \\ &\geq3\times\sqrt[3]{\sqrt{k^2+1}\cdot\sqrt{k^2+1}\cdot\frac{8}{k^2+1}} \\ &=6.\end{aligned}$
注:对非负数$a,b,c$,有$\boldsymbol{\frac{a+b+c}{3}\geq\sqrt[3]{abc}}$.
若不用基本不等式,可以用换元。令$t=\sqrt{k^2+1}$,则原式$=2t+\frac{8}{t^2}$,求个导,注意$t$的取值,也能算出来。但还是直接用基本不等式更快。
当且仅当$\sqrt{k^2+1}=\frac{8}{k^2+1}$,即$k=\pm\sqrt{3}$,最小值为$6$.
法二:由阿基米德三角形性质1和性质3得 $P(\frac{x_1+x_2}{2},-1)$,也可求出$|PF|$,做法与法一同。
抛物线焦点弦
过抛物线$y^2=2px(p>0)$的焦点$F$作一条直线$L$和此抛物线交于$A(x_1,y_1),B(x_2,y_2)$两点。
性质
性质0:$|AB|=x_1+x_2+p$
性质1:若直线$L$的倾斜角为$\theta $,则弦长$\boldsymbol{|AB|=\frac{2p}{sin^2\theta }}$
证明:若$\theta \neq\frac{π}{2}$时,直线$L$的方程为:$y=tan\theta (x-\frac{p}{2})$即$x=y\cdot cot\theta +\frac{p}{2}$,代入抛物线方程得$y^2-2py\cdot cot\theta -p^2=0$,由韦达定理得$\boldsymbol{y_1y_2=-p^2,y_1+y_2=2pcot\theta }$.
由弦长公式得$|AB|=\sqrt{1+cot^2\theta }$,$|y_1-y_2|=2p(1+cot^2\theta )=\frac{2p}{sin^2\theta }$
对于抛物线$x^2=2py$,弦长$|AB|=\frac{2p}{cos^2\theta },x_1x_2=-p^2$.
性质2:过焦点的弦通径长最短.
性质3:$\boldsymbol{S_{ΔOAB}=\frac{p^2}{2|sin\theta |}}$
$\frac{S^2_{ΔOAB}}{|AB|}=\frac{p^3}{8}$为定值.
对于抛物线$x^2=2py$,把$sin\theta $换成$cos\theta $即可.
性质4:$\boldsymbol{x_1x_2=\frac{p^2}{4}}$

性质5:以$AB$为直径的圆与抛物线的准线相切.(易证)
设$M$为$AB$的中点,过$A$点作准线的垂线$AA_1$,过$B$点作准线的垂线$BB_1$,过$M$点作准线的垂线$MM_1$,由梯形的中位线性质以及抛物线的定义知:
$|MM_1|=\frac{|AA_1|+|BB_1|}{2}=\frac{|AF|+|BF|}{2}=\frac{|AB|}{2}$
性质6:过$A$作准线的垂线$AA_1$,过$B$作准线的垂线$BB_1$,连$A_1F$,$B_1F$,则$\boldsymbol{A_1F\bot B_1F}$.
性质7:(1)$\boldsymbol{AM_1\bot BM_1}$
(2)$\boldsymbol{M_1F\bot AB}$
(3)$\boldsymbol{|M_1F|^2=|AF|\cdot |BF|}$(相似可证)
(4)如图2-1,$M_1,Q,F,H$四点共圆.

性质8:(1)$\boldsymbol{A,O,B_1}$三点共线.(2)$\boldsymbol{B,O,A_1}$三点共线.
证明:因为$k_{OA}=\frac{y_1}{x_1}=\frac{y_1}{\frac{y_1^2}{2p}}=\frac{2p}{y_1}$,$k_{OB_1}=\frac{y_2}{-\frac{p}{2}}=-\frac{2y_2}{p}$,而$y_1y_2=-p^2$,所以$k_{OA}=k_{OB}$,所以三点共线。同理可证(2)。
性质9:$\boldsymbol{\frac{1}{|FA|}+\frac{1}{|FB|}=\frac{2}{p}}$
证明:过$A$点作$AR$垂直于$x$轴于$R$,过$B$点作$BS$垂直于$x$轴于点$S$,设准线与$x$轴交点为$E$,直线$L$的倾斜角为$\theta $.
则$|ER|=|EF|+|FR|=p+|AF|cos\theta =|AF|$,$\boldsymbol{\therefore|AF|=\frac{p}{1-cos\theta}}$,同理可得$\boldsymbol{|BF|=\frac{p}{1+cos\theta}}$,得证。
椭圆
椭圆的三大定义
椭圆第一定义:(略)
椭圆第二定义:把平面内到一定点$F$的距离与到一定点$l$的距离之比为一常数$e(0<e<1)$点的轨迹叫椭圆.经过计算可得准线方程:$\boldsymbol{x=\pm \frac{a^2}{c}}$.
椭圆第三定义:把平面内到两个定点$A_1,A_2$的斜率乘积为一个常数$e^2-1(-1<e^2-1<0)$点的轨迹叫做椭圆.
椭圆第二定义
焦半径公式推导:
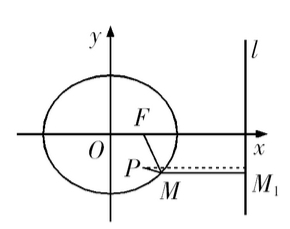
在该椭圆中,$F$为焦点,$l$为准线,$M(x,y)$为椭圆上一点,过$M$作$MM_1$交$l$于$M_1$. 设$FM$与$x$轴正半轴的夹角为$\theta$,设$F$到$l$距离为$p$.
结论:$\boldsymbol{FM=\frac{ep}{1+e\cdot \cos \theta}=a-e\cdot x}$
证明:设FM=r,由椭圆第二定义知$MM_1=\frac{r}{e}$.
则$p=r\cdot \cos \theta +\frac{r}{e}$.
$FM=\frac{ep}{1+e\cdot \cos \theta}$.
$\because \frac{|FM|}{|MM_1|}=e$.
$\therefore |FM|=e|MM_1|=e\cdot (\frac{a^2}{c}-x)=a-ex$.
证毕.